Pisut selleaastastest lõputöödest: matemaatika ja statistika magistriõppe matemaatilise statistika eriala
Matemaatika ja statistika magistriõppe matemaatilise statistika erialal kaitsti selle suve alguses kuut tööd, millest tutvustame seekord kaht. Tuuli Jürgenson kirjutas oma magistritöö teemal „Retrospektiivsete ja prospektiivsete andmete kombineerimine ülegenoomsetes seoseuuringutes“ ning teda juhendasid doktorant Anastassia Kolde, professor Krista Fischer ja professor Reedik Mägi. Kristin Avansi töö kannab pealkirja „Paarikaupa Markovi mudel: definitsioon ja näited“ ning tema juhendaja oli professor Jüri Lember.
Kuidas sinu töö sündis? Kas leidsid töö teema ise või pakuti seda sulle instituudi poolt?
Tuuli: Magistritöö on seotud minu tööga Tartu Ülikooli Eesti Geenivaramus. Töö teema lähtus geenivaramus sageli esinevast olukorrast, kus ühte analüüsi on vaja kaasata kahte erinevat tüüpi andmed. Samal ajal pole selge, kuidas sellisel juhul andmeid omavahel kombineerida ja millist analüüsimeetodit kasutada. Minu töö eesmärk oli erinevaid meetodeid võrrelda ja selgitada välja parim.
Kristin: Läksin oma bakalaureuseaegse juhendaja jutule ja küsisin, kas saaksin ka magistritööks mõne huvitava teema. Kuna bakalaureusetöös uurisin varjatud Markovi mudelit, siis juhendaja pakkus välja, et edasi võiks vaadata üldisemat mudelite klassi, milleks on paarikaupa Markovi mudel (PMM).
Mida sa oma lõputöös uurisid ning mida teada said?
Tuuli: Täpsemalt uurisin ma oma töös, kuidas on kõige parem analüüsida seost mõne riskifaktori ja haiguse vahel, kui kasutada on nii retrospektiivsed kui prospektiivsed haigestumisandmed. Retrospektiivseteks ehk jälgimiseelseteks haigestumisteks nimetasime me selliseid haigusjuhtumeid, mis olid toimunud enne seda, kui inimene mõne uuringuga, näiteks geenivaramuga, liitus. Prospektiivsed ehk jälgimisaegsed haigestumised on aga need, mis on toimunud pärast seda, kui inimene on uuringuga liitunud. Töös selgus, et jälgimiseelseid ja jälgimisaegseid andmeid võib analüüsida koos, kasutades lihtsat binaarse uuritava tunnuse mudelit, näiteks logistilist regressioonimudelit.
Kristin: Töö põhieesmärk oli uurida konkreetseid näiteid nii diskreetsetest kui ka pidevatest PMM-dest. Alustasin mudeli definitsiooni ning teiste vajalike mõistete tutvustamisega. Edasi uurisin erinevaid näiteid ja tegin kindlaks, kuidas neid klassifitseerida, kirjeldasin tähtsamaid erijuhte ning tõestasin valitud mudelite omadusi.
Kuvatõmmis Tuuli lõputööst. Joonisel on kujutatud teist tüüpi diabeedi ja kaheksa geenivariandi vahelised seosed (hinnangud 95%-usaldusintervallidega) erinevate võrreldud analüüsimeetodite korral.
Mis oli sinu jaoks kõige huvitavam tulemus, mis tööst välja tuli?
Tuuli: Huvitav oli see, et kuigi töös rakendasime ka oluliselt keerukamaid meetodeid – mille tarvis analüüsiti retrospektiivseid ja prospektiivseid andmeid eraldi, rakendati nii elukestusanalüüsi meetodeid kui binaarse uuritava tunnuse mudelit ja meta-analüüsi – siis parima tulemuse andis ikkagi lihtne meetod, mille puhul analüüsitakse nii retrospektiivseid kui prospektiivseid andmeid koos, kasutades binaarse uuritava tunnuse mudelit.
Kristin: PMM-id on väga üldine klass, mis võimaldab uurida erinevaid keerulise sõltuvusstruktuuriga andmeid. Huvitav oli näha, kuidas mudeli ning parameetrite sobival muutmisel saame modelleerida väga erinevaid protsesse. Samuti oli põnev leida erijuhte, kus üks mudeliklass taandus teiseks.
Miks on sinu valitud teema uurimine oluline? Kas ning kuidas sinu töö tulemusi edaspidi kasutatakse?
Tuuli: Olukord, kus analüüsi saaks kaasata nii retrospektiivsed kui prospektiivsed andmed, on väga levinud (näiteks ülegenoomsete seoseuuringute puhul) nii geenivaramus, aga ka teistes suurtes biopankades üle maailma. Seega on oluline teada, millised meetodid töötavad selliste andmete uurimisel kõige paremini.
Kristin: PMM-d hõlmavad endas mitmeid praktikas rakendatavaid mudeleid, näiteks saab neid kasutada kõnetuvastuses, piltide tuvastamisel, mitmesuguste majandusülesannete lahendamisel. Minu töö annab üldise ülevaate PMM-st, seega võib seda kasutada õppematerjalina teemast ülevaate saamiseks. Samuti võib edaspidi toodud näiteid üldistada, leida uusi ning uurida ka mudeli keerulisemaid omadusi.
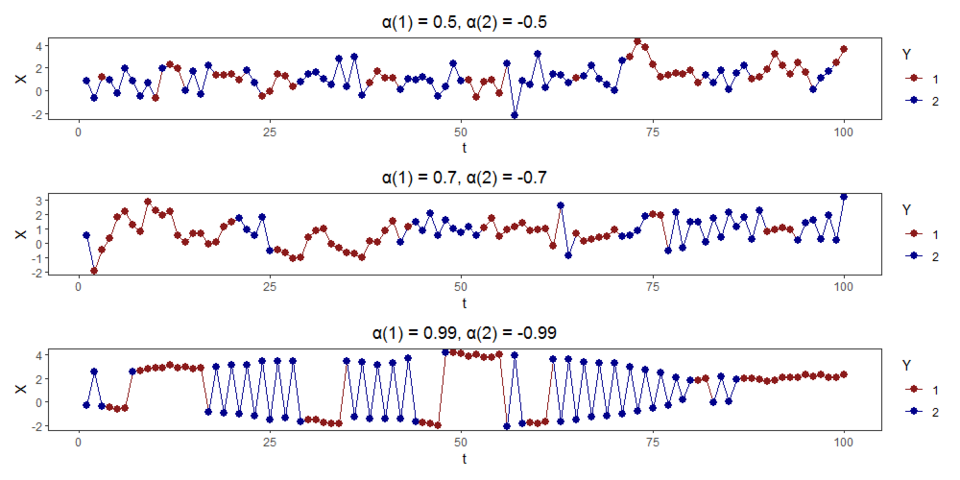
Kuvatõmmis Kristini tööst. Näide PMM-st, kus X1, X2, ... on sama jaotusega mittekorreleeritud juhuslikud suurused, kuid mitte sõltumatud, parameetrite sobival muutmisel saame reguleerida nende sõltuvust.
Kas soovid miskit veel lisada?
Kristin: Statistika eriala lõputööd on enamjaolt väga praktilised, kuid julgustan tudengeid valima ka teoreetilisemaid teemasid. Kuigi hetkel võib tunduda, et teoreetilistel töödel pole praktilist väärtust, siis tulevikus leiavad need kindlasti rakendust.
Tuuli ja Kristini lõputöid saab lugeda siin ja siin. Matemaatika ja statistika instituudi kõik selleaastased lõputööd leiab meie veebist.